bionsyn.blogg.se

1. #FREE42 TRIG FUNCTIONS DISAPPEARED CODE#
2. #FREE42 TRIG FUNCTIONS DISAPPEARED PLUS#
3. #FREE42 TRIG FUNCTIONS DISAPPEARED PROFESSIONAL#
4. #FREE42 TRIG FUNCTIONS DISAPPEARED WINDOWS#

Personally, I don't like it very much that 1/7 + 1/7 + 1/7 + 1/7 + 1/7 + 1/7 + 1/7 does not come out as 1, but that's life, or rather, that's limited precision.

Presumably you're going to round money amounts to two decimals before printing your bill? :-)īut all kidding aside, outside of financial applications, all you're dealing with in the example given above is a misconception of how computers store numbers, and about the limits of precision.

#FREE42 TRIG FUNCTIONS DISAPPEARED PLUS#

I can understand it for financial applications, I guess, but even there it's hard to see what problem would be caused by having $2 plus 5 times 20 cents minus $3 come out less than one tenth of one trillionth of a cent wrong. I don't understand what the fuss is about. And even today, programming in C or FORTRAN or Java it's the same. I started computer programming on a Commodore PET, 28 years ago, and one of the first things I noticed were numerical quirks like that. I suppose it depends on what you're used to. 2 + 3 - you get 8.8818e-16 also, 1 enter 1e-13 + 1 - to get 9.9920e-14 both of these are really annoying. here are some things that increasingly bug me (and you). how nasty!īut more and more recently i am going away from binary back to bcd. ok, so then after effectively converting to decimal, i can algorithmically treat each part (M and E) separately eg mod(mod(M,r) + mod(10^E,r), r). what then happens, is that digits below M in significance are regarded as zero, although they wouldn’t be zero if kept in binary (there is implied decimal garbage if multiplied). so anyway, what im doing is temporarily recasting X into a decimal form but i store M in my floating point representation even though it is actually an integer (that’s because ints arn’t big enough). some decimal systems work entirely like this (ie using a binary mantissa), but the problem is that you have to cope with denomalised numbers. this is another way to tackle bcd, ie to have a binary integer mantissa and a power of 10 exponent. what i did in the end, and this approach works with similar decimal problems, is to decimalise the number by re-representing binary X by M*10^E where M is a binary integer. i had real trouble fixing this in scicalc for the same binary reasons. for example 1e50 enter 9 mod, comes out at 3 instead of 1. this is a bug.Īlso, binary is hampering mod.

#FREE42 TRIG FUNCTIONS DISAPPEARED WINDOWS#

can you supply the bmp resource files to build the windows version.

Lastly, thanks for writing this calculator!

#FREE42 TRIG FUNCTIONS DISAPPEARED CODE#

i can give you some c code for ridders if you like, but i just cribbed it from numerical algorithms in C. it was part an attempt to recreate the missing solve and integ features on the hp9gĪlso, i had a substantial improvement for solve by moving from the secant method to ridder’s method as described there. this code i developed by trying to reverse engineer the method used on the 15c and it performs about the same, I see you need a ln1(x) = ln(x+1), here’s one i wrote for scicalc,Īlso, i can suggest a better integ algorithm. I have an alternative implementation of the gamma function you might like, i did the same in my implementation of scicalc but more and more recently i am going away from binary back to bcd.

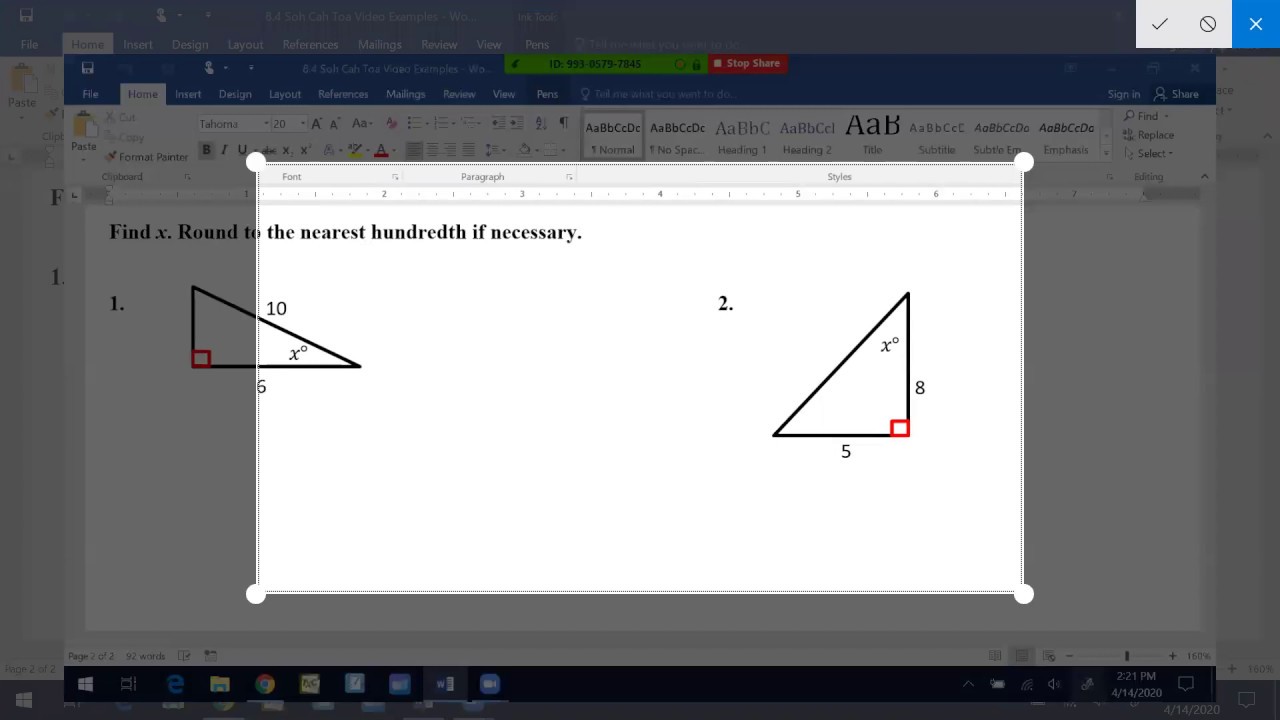
i can well understand your use of ieee754 not least from a performance point of view. firstly, your wrestle with bcd vs binary is something ive been struggling with for some time. I have a few ideas that might help it to become even better. i like the palm version, it works well, although the beep is a bit loud. Whether or not you would like it would probably mostly depend on whether you can forgive its long list of bugs (which include failing to calculate trigonometric functions accurately for angles close to multiples of 90 degrees), which HP never seems to have bothered to fix.This is really cool indeed. HP's line of high-end scientifics ended with the HP-42S. In context this makes the HP-35S a mid-range scientific calculator. It is named after the original HP-35 but by lineage it's a replacement for the HP-33S and descends from the HP-32S and HP-32SII models from the late 1980s and 1990s.

#FREE42 TRIG FUNCTIONS DISAPPEARED PROFESSIONAL#

It has been in continual production since then, presumably because it's one of only a few scientific calculators allowed in some professional engineering exams in the US.

HP introduced it in 2007 to commemorate the 35th anniversary of their first pocket scientific calculator, the HP-35. I bought one of these that I saw in a shop about a decade ago. The guts are modern but the UI is the same classic design. They made a retro tribute to one of the HP calculators a few years ago.